Given a binary tree, check whether it is a valid binary search tree.

Prerequisites

Before we go forward, it would be better to have some prior knowledge about binary search trees. Go through links given below, to get a good understanding of binary search trees.

Introduction to Binary trees

Introduction to Binary Search trees

Note : In this post, the abbreviation BST is used to refer to a binary search tree.

Approach

Given that you have a good understanding of BST, we all know that a BST satisfies the following property

For each node N

1. All nodes in the left subtree of N have a value smaller than N
2. All nodes in the right subtree of N have a value greater than N
3. The left & right subtrees of N should be valid BSTs.

Now the challenge is to efficiently validate the above properties for every node of a tree.

Let us try to analyze this problem by looking at a valid BST given below

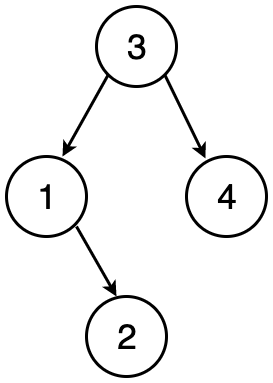
We can clearly notice that this tree satisfies all the properties discussed above.

Let us say we want to traverse from the root of the tree and reach node 2. The path would be 3 → 1 → 2 where 3 > 1 and 1 < 2

Thus, every node N in the BST can be mapped to a min and max value where the value of all the tree nodes with N as root lies within the interval [min, max]

Therefore in order to decide whether a BST is valid, for each node we compute this interval and check whether the above mentioned property is satisfied. So now the question is how do we compute this interval?

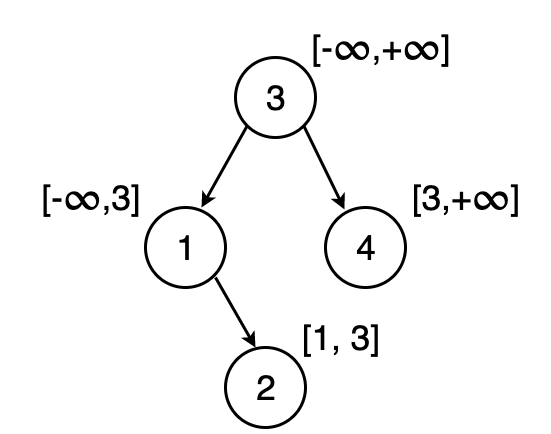
Let us get back to the example of valid BST.

We start at node 3. Since node 3 is the root, it can have any value. So the interval for node 3 would be [-\(\infty\), \(\infty\)].

Now we would like to compute the interval for node 1. Since node 1 is the left child of node 3, all the nodes with 1 as root can have a maximum value of 3. Therefore the max value for node 1, would be 3 and thereby the interval for node 1 is [-\(\infty\), 3].

Similarly, since node 4 is on the right of node 3, all the nodes with 4 as root should a minimum value of 3. Therefore the min value for node 4, would be 3. Thus the interval for node 4 is [3, \(\infty\)].

We repeat the same procedure to compute the intervals for each node recursively and check whether the node’s value lies within its interval.

The intervals for the above BST

Code

Below is the java implementation for the above discussed solution on InterviewBit.

Time Complexity

In this implementation, every node is visited exactly once in the worst case.(when the given binary tree is a valid BST). Therefore the time complexity is O(n), where n is the number of nodes in the binary tree.

Space Complexity

This implementation does not use any additional space. So the space complexity is O(1).

Other Info

This is an interview question asked by Facebook & Amazon. This problem can also be tried out on LeetCode.